Assignment




Solution
Answers part 1:
1: F
2: F
3: T
4: T
5: F
6: T
7: T
8: T
9: F
10: T
11: T
12: T
13: F
14: F
15: F
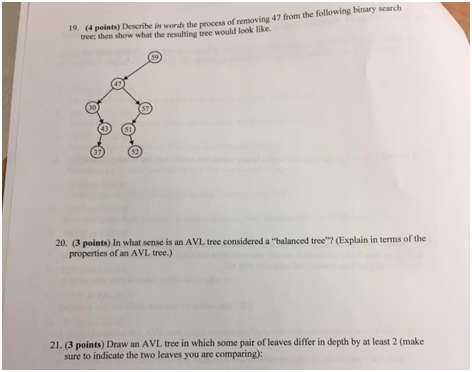
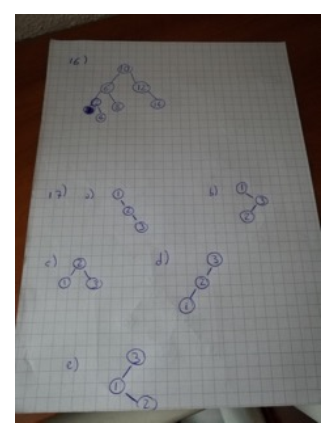
16-17: image
18:
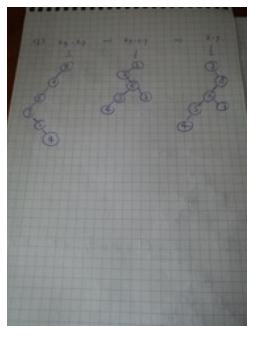
Base: For N=1N=1 the proof is simple, we can see that the number of leaves =1=1 and the numberof internal vertices =0=0, 0 + 1 = 1 thus the assumption is correct for the base case.
Assume: We'll assume that for N∈NN∈N the number of leaves is greater by one than the numberof internal vertices, and prove for N+2N+2 (since N+1N+1 will make the tree non-full).
Proof: Let TT be a full binary tree over N+2N+2 leaves. We'll arbitrary choose an internal vertice
and trim it's leaves, now we have TʹTʹ a tree on NN leaves and according to the assumption we
know that the number of leaves is larger by 11 than the number of internal vertices. If we let n
ʹ1n1ʹ be the number of leaves in TʹTʹ and nʹ2n2ʹ be the number of internal vertices in TʹTʹ we get
that nʹ1=nʹ2+1n1ʹ=n2ʹ+1 from the assumption. Now if we recover the trimmed leaves we get that:
n1=nʹ1-1+2=nʹ1+2n1=n1ʹ-1+2=n1ʹ+2
n2=nʹ2+1n2=n2ʹ+1
And since the proportions are kept, we know that n1=n2+1
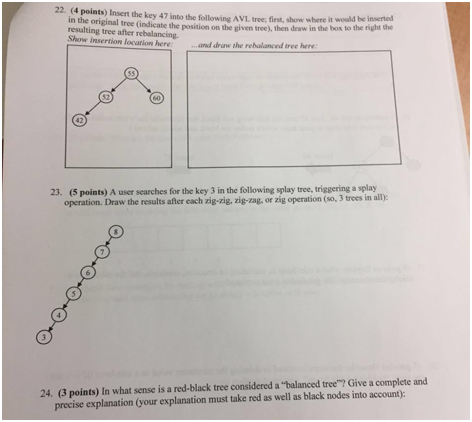
19: image

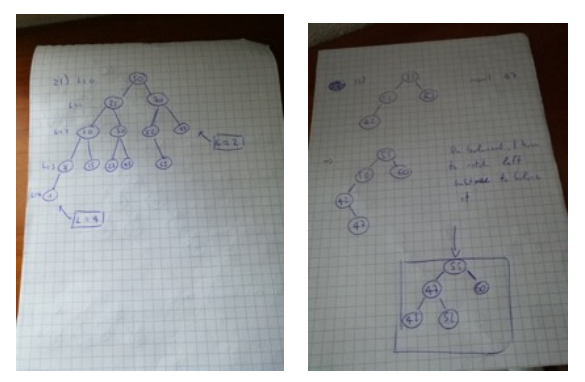
20: AVL is said to be balanced because the difference in height between the left and the right
subtree of a node is at most 1
21-22-23: image
24:
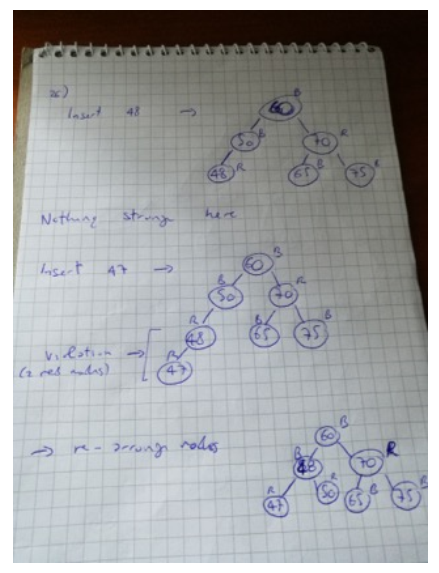
Redblack trees are said to be balanced because at any time the length of the longest path from rootto leaf is at most twice the length of the shortest path.
25:
1. -Initially, root node is black
2. Leaves are black and contain the null value
3. Both children of a red node are blak nodes
4. Each path from root to leaf contains the same amount of black nodes
26: image
27:
Min-heap is a tree-based data structure, in which the key of a node is always greater than or equalto the key of the node's father. Heap is the most efficient implementation of the priority queuestructure, and is usually implemented as a binary tree whose root is the smallest value. There is noimplied ordering between sibling nodes and no implied order for a traversal.
28:
Since the minimum value is stored in the root of a minheap, to delete the minimum value the root
must be deleted. Then, the last value in the array is copied to the root, and it is taken to its place
with a sifting procedure:
1. if it has no children, sifting is over
2. if it has one child, check if the heap property is broken and if it is swap its position withi its
child's, and sift down the child.
3. If it has two children, choose the smallest and swap-sift if the heap property is broken
29:
To find the max value in a minheap, I would insert the value with inverted sign. This would allowme to find the maximum as I would have found the minimum and this would maintain the sametime complexity for the insert-delete-retrieval operations.
30:
Navigate the tree knowing that each level can be a min or a max level
31:
the goal of a good hash function is to map a set of values in a smaller set avoiding as much as
possible to have different values mapped into the same key.
32: image

33:
Open addressing (probing): finding the closest empty bucket in case of conflicts
Chaining: consists of an array in which each slot contains the link to a single linked list containingkey-value pairs with the same hash. When a new value with the same hash is inserted, it isappended at the end of the corresponding list
34:
intextractMin()
{
if (heap_size<= 0)
return INT_MAX;
if (heap_size == 1)
{
heap_size–;
return heap_data[0];
}
// Store the minimum value, and remove it from heap
introot = heap_data[0];
heap_data [0] = heap_data[heap_size-1];
heap_size–;
MinHeapify(0);
return root;
}
// A recursive method to heapify a subtree with root at given index
void MinHeapify(inti)
{
intl = left(i);
intr = right(i);
intsmallest = i;
if (l
smallest = l;
if (r
[r]
smallest = r;
if (smallest != i)
{
swap(&heap_data[i], &heap_data[smallest]);
MinHeapify(smallest);
}
}
void swap(int*x, int*y)
{
inttemp = *x;
*x = *y;
*y = temp;
}